In diesem Artikel betrachte ich die verschiedenen Formen der Verzinsung, die einmalige, die jährliche, dann die unterjährige und schließlich die stetige Verzinsung. Wie stehen stetige und jährliche Zinssätze in Relation? Im Anschluß gehe ich näher auf die stetige Verzinsung ein, wie gehe ich mit variablen Zinssätzen um oder was ist bei negativen Zinssätzen.
Zum Schluss gebe ich noch ein zusammenfassendes Fazit.
Einmaliger Zins
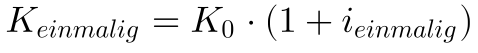
Jährlicher Zins
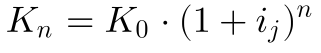
Auch wenn hier vom jährlichen Zins gesprochen wird, kann die Zinsperiode eigentlich beliebig festgelegt werden. Der Zins i wurde für eine Zinsperiode n=1 definiert. Üblich geht man von einer jährlichen Verzinsung aus, weswegen hier diese Bezeichnung gewählt wurde. Bei langen Laufzeiten wirkt sich der Zinseszinseffekt immer stärker aus.
Unterjähriger Zins
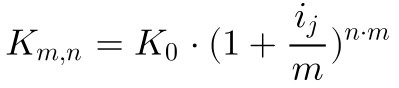
Der Zins i wurde für die Zinsperiode n = 1 definiert und dann in m Zinsperioden unterteilt. Da meist von einer jährlichen Zinsperiode ausgegangen wird, wurde hier die Bezeichnung unterjähriger Zins gewählt.
Je kürzer die Zinsperiode gewählt wird, umso höher die Verzinsung bei gleichem jährlichen Zinssatz. Der Wert konvergiert, der Grenzwert wird beim stetigen Zins erreicht.
Stetiger Zins
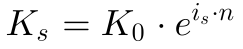
Der stetige Zins wird auch hier für eine Zinsperiode n=1 definiert. Die Formel für den stetigen Zins ist auch bei negativen Zinssätzen gültig.
Äquivalente Zinssätze zwischen jährlichen stetigem und jährlichen Zinssatz
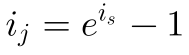
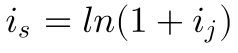
Stetige Verzinsung
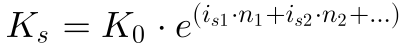
Die Reihenfolge der Zinsperioden ist unerheblich.

Grundlagen
Ich möchte hier auf die verschiedenen Formen der Zinsrechnung eingehen, ohne aber mathematisch in die Tiefe zu gehen. Als schöne Übersicht empfehle ich die Abhandlung von Prof. Dr. Klaus Gach[1].
Einmalige Verzinsung
Bei einer einmaligen Verzinsung beschließen zwei Vertragspartner den Verleih von Geld gegen einen festen einmaligen Zinssatz. Also beispielsweise leiht Herr Müller an Herrn Schmitz 1000 Thaler für 2 Jahre und nach zwei Jahren zahlt Herr Schmitz das Darlehen zurück mit einer Verzinsung von 8%.
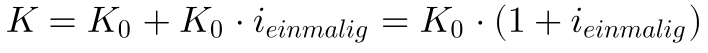
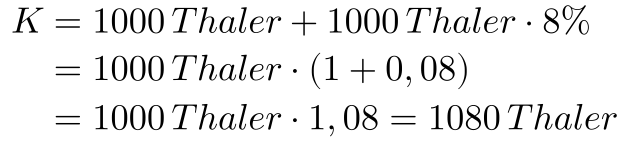
Also nach zwei Jahren zahlt Herr Schmitz an Herrn Müller 1080 Thaler und damit ist das Darlehen mit Zinsen getilgt.
Jährliche Verzinsung
Nehmen wir nun an, daß Herr Müller an Herrn Schmitz wieder 1000 Thaler für 2 Jahre leiht, aber nun vereinbaren die beiden eine jährliche Verzinsung von 4%. Das heißt nach einem Jahr wird ein Zins von 4% fällig, aber dieser Zins wird nicht ausgezahlt, sondern geht in die Darlehenssumme für das zweite Jahr ein.
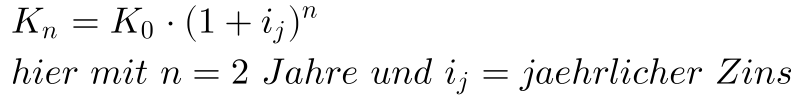
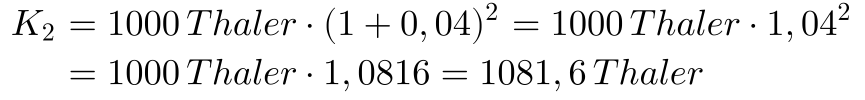
Wie man sieht ist der Endbetrag etwas höher als im ersten Fall, dies liegt am Zinseszinseffekt. Im 2. Jahr wird auch der Zins des ersten Jahres mit verzinst und damit kommt es zu der geringen Differenz. Übrigens könnte man hier auch den Zins für 2,5 Jahre mit der gleichen Formel berechnen, es gilt:
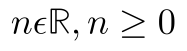
Läßt man n jetzt sehr groß werden, also berechnet man den Wert für lange Laufzeiten, dann wird der Zinseszinseffekt riesige Ausmaße annehmen. Nehmen wir für obiges Beispiel eine Laufzeit von 100 Jahren an, dann ergibt sich:
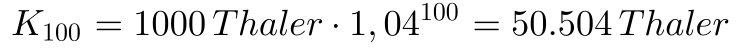
Bei 500 Jahren Laufzeit sind wir bei:
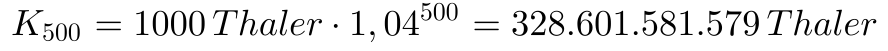
Würde man im letzten Beispiel aber den Zins immer beiseite legen und nicht neu anlegen, dann würde 500 Jahre lang, jedes Jahr 4% auf 1000 Thaler anfallen, also 500 mal 40 Thaler, damit 20.000 Thaler.
Unterjährige Verzinsung
Eine weitere Variante bei der Zinsrechnung ist die unterjährige Zinsperiode, also der Zins wird beispielsweise jedes halbe Jahr, quartalsweise, jeden Monat oder gar jeden Tag, Stunde oder Minute berechnet. Bezogen auf das obige Beispiel, nehmen wir an, daß Herr Müller an Herrn Schmitz wieder 1000 Thaler für 2 Jahre leiht, aber nun vereinbaren die beiden eine monatliche Verzinsung von 0,333…%, dies entspricht einem Zins von 8% geteilt durch 24 Monate. Das heißt nach jedem Monat wird ein Zins von 0,333…% fällig, aber dieser Zins wird wieder nicht ausgezahlt, sondern geht in die Darlehenssumme für das nächste Jahr ein.
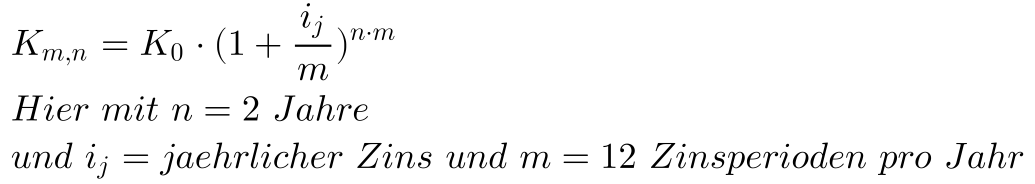
Der Buchstabe m paßt hier zufällig zur monatlichen Zinsperiode, aber genausogut könnte m auch 4 sein, für eine quartalsmäßige Zinsperiode. Zudem ist es egal ob ich,
a) von einer Zinsperiode von 2 Jahre ausgehe, mit einem Zweijahreszinssatz von 8% und 24 Zinsperioden für 2 Jahre.
oder
b) von einer Zinsperiode von 1 Jahr ausgehe, mit einem Jahreszinssatz von 4% und 12 Zinsperioden pro Jahr. Diese gebräuchlichere Variante habe ich in den Formeln angewendet.
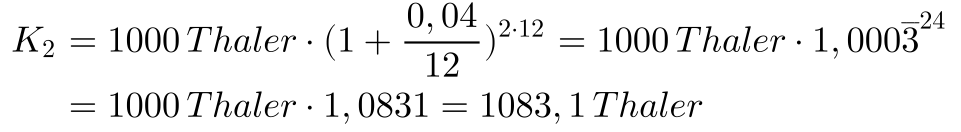
Es sollte jetzt auch klar geworden sein, daß das Teilen des einfachen Zinses durch 24 Monate, hier von 8% für 2 Jahre, nicht zu einem äquivalenten Zins führt, denn am Ende muß Herr Schmitz ja, für die gleiche Summe und Laufdauer, mehr Zinsen zahlen. Auf dieses Thema wird im Anschluß noch eingegangen.
Stetige Verzinsung
Wir haben gesehen, daß mit mehr Zinsperioden, die zu zahlenden Zinsen immer weiter ansteigen. Was würde jetzt passieren, wenn wir, nach dem Muster der unterjährigen Zinsperioden, unendlich viele Zinsperioden pro Jahr hätten, aber gleichzeitig der Zinsbetrag pro Zinsperiode gegen Null streben würde? Am Ende soll ja der aufaddierte Gesamtzins aller Zinsperioden eines Jahres dem Jahreszins entsprechen. Würde dann auch der zu zahlende Zins ins Unendliche steigen oder gäbe es einen konvergierenden Wert?
Ausgehend von der unterjährigen Zinsformel,
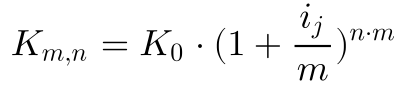
definieren wir jetzt den Wert,
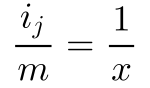
den wir in obige Formel einsetzen,
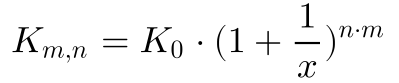
mit
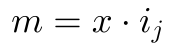
wird daraus:
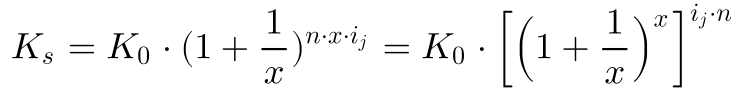
Jetzt betrachten wir gesondert den Term:
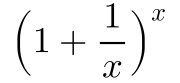
für x gilt bei einem positivem Jahreszins:
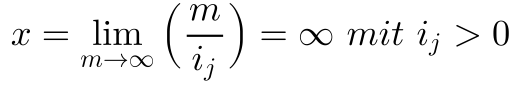
Der Grenzwert dieser Funktion ist die Eulersche Konstante e.
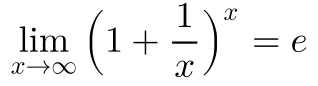
Diese bisherige Herleitung habe ich dem oben erwähnten Dokument entnommen. Da für negative Zinsen keine Aussage getroffen wurde, war ich nicht sicher, wohin die Limesfunktion dann konvergiert. Deshalb hier eine etwas andere Vorgehensweise, ich forme den obigen Term wieder um, indem ich x ersetze:
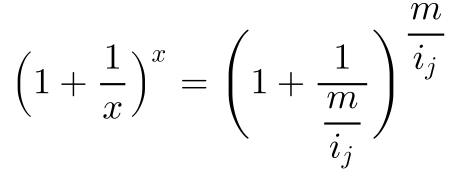
Daraus ergibt sich folgende Formel:
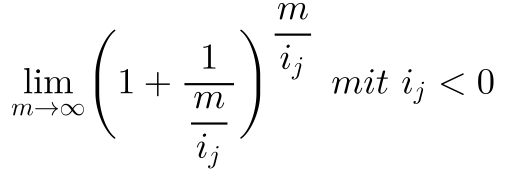
Diese gebe ich so bei WolframAlpha ein, das i ersetze ich durch ein -a, damit es nicht fälschlicherweise als die komplexe Zahl i interpretiert wird:
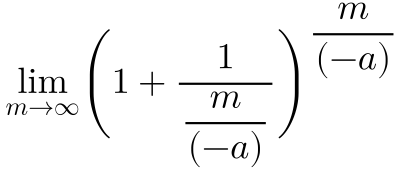
Das Ergebnis lautet:
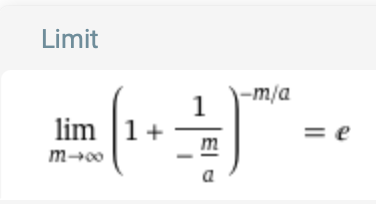
Zur Sicherheit nehme ich jetzt einen negativen Jahreszins von 5% an:
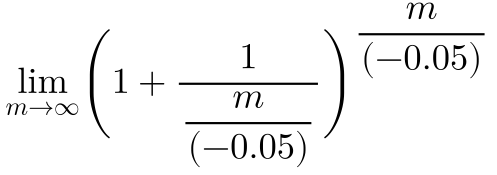
Das Ergebnis lautet:
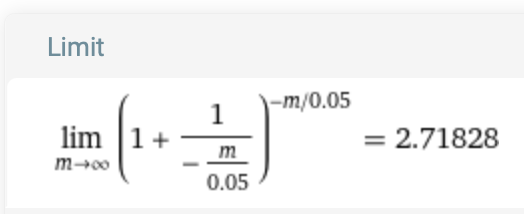
Das ist für mich jetzt hier Beweis genug, daß auch bei negativem Zinssatz die Eulersche Zahl als Ergebnis herauskommt. Wir sehen hier auch schön, daß der Jahreszinssatz, sofern er ungleich 0 ist, überhaupt keinen Einfluß auf das Ergebnis hat.
Somit lautet das Ergebnis für die stetige Verzinsung
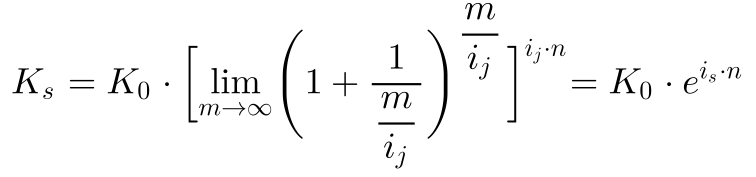
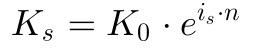
Bei unendlich vielen Zinsperioden in einem Zeitraum ist das Ergebnis endlich, es konvergiert also. Da das Ergebnis nicht dem Jahreszins entspricht, habe ich den Zinssatz zur klaren Unterscheidung in 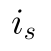
Nehmen wir nun erneut an, daß Herr Müller an Herrn Schmitz 1000 Thaler für 2 Jahre leiht, aber nun vereinbaren die beiden eine stetige Verzinsung bei einem stetigen jährlichen Zins von 4%. Das heißt auch hier, dieser Zins wird wieder nicht ausgezahlt, sondern geht immer wieder in die Darlehenssumme ein.
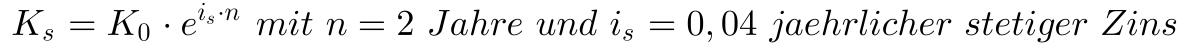
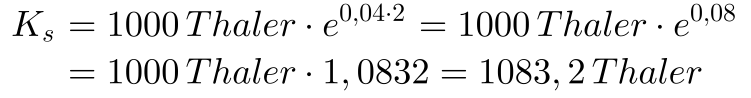
Auch hier steht es mir natürlich frei, statt einer jährlichen, eine zweijährige Zinsperiode zu wählen. In diesem Fall wäre n = 1 und würde den Zweijahreszeitraum abdecken und der Zinssatz läge für diese zwei Jahre bei 8%. Möchte ich in diesem Fall das verzinste Kapital nach einem Jahr wissen, dann muß ich n = 0,5 setzen. Somit brauche ich auch beim stetigen Zins immer noch die Information, wie lang die Zinsperiode ist, für die der stetige Zins definiert wurde. Im Regelfall wird es aber ein jährlicher stetiger Zins sein.
Wir sehen, der Zinsaufschlag gegenüber der monatlichen Zinsperiode hält sich in Grenzen. Die stetige Verzinsung hat aber den Vorteil, daß wir uns nicht mehr mit einzelnen Zinsperioden rumschlagen müssen, ich kann zu jedem Zeitpunkt mit der Verzinsung starten und aufhören. Somit ist dies eigentlich die eleganteste Methode mit Zinsen zu rechnen.
Nun zur Berechnung eines äquivalenten jährlichen Zinses zwischen jährlicher Verzinsung und stetiger Verzinsung. Die Bezeichnung Jahreszins ist eigentlich nicht ganz genau, denn theoretisch läßt sich die Jahreszinsformel auch für anders definierte Zinsperioden anwenden. Wichtig ist nur, daß der Zins i für die Zinsperiode n = 1 definiert wurde. Entsprechend bezieht sich der äquivalente stetige Zins dann auf die gleiche Zinsperiode. Da aber in der Praxis meist von einem Jahreszins ausgegangen wird, wollen wir es hier dabei belassen.
Bei der Berechnung des äquivalenten Zinses muß die Bedingung erfüllt sein, daß nach der Laufzeit das gleiche Kapital erwirtschaftet wird.
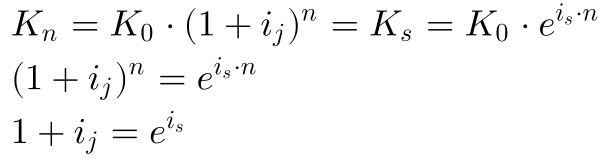
Den äquivalenten Jahreszins kann man so aus dem jährlichen stetigen Zins berechnen.
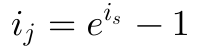
Und den äquivalenten jährlichen stetigen Zins kann man wie folgt aus dem Jahreszins berechnen.
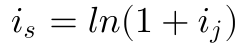
Testen wir das kurz aus, zur Erinnerung bei 2 Jahren Laufzeit und einem Jahreszins von 4% ergab sich folgendes Kapital.
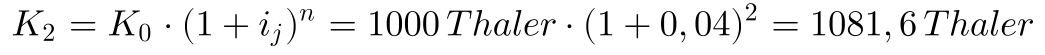
Der äquivalente stetige Zins berechnet sich zu:
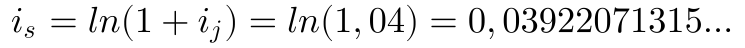
Damit berechnet sich das Kapital mit Hilfe des stetigen Zins zu:
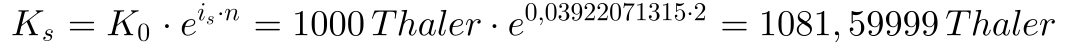
Bis auf einen Rundungsfehler entspricht dies genau unseren Erwartungen.
[1] Auf der Webseite von Prof. Dr. Klaus Gach vom 09.03.2023:
https://www.klaus-gach.de/dateien/wire/zz03.pdf
